EL REPARTO DE LOS MARINEROS |
Llamando X al número de monedas que había veamos el reparto: |
El primero se lleva (x-1)/3 y tira una al mar. Quedan x-[(x-1)/3]-1=(3x-x+1)/3-1= (2x+1)/3-1=(2x-2)/3 |
El segundo se lleva [(2x-2)/3-1]3= (2x-5)/9 Arroja una al mar quedan (4x-10)/9 |
El tercero [((4x-10)/9)-1]3=(4x-19)/27 Arroja una y quedan (8x-38)/27 |
Reparto final [(8x-38)/27)-1]3= (8x-65)/81 y se queda una el que reparte. |
Por tanto el numero inicial de monedas es múltiplo de 81; el único entre 200 y 300 es el 243, pero como las divide entre 3 y queda una de resto el número buscado es el 241 |
El primero se lleva 240/3=80; arroja una, quedan 160; El segundo 159/3=53; arroja una y quedan 106 |
El tercero se lleva 105/3=35, arroja una, quedan 70; en el último reparto se queda una y 23 para cada uno |
Así pues se levan: (80+23)=103: (53+23)=76; (35+23)=58, 3 arrojadas al mar y una guardada que suman las 241 |
 |
DIFÍCIL REPARTO |
Viendo que tendrían que sacrificar algún camello acuden al Juez. Este les regala un camello con lo cual ahora tienen 36. |
El primero se lleva 1/9 de los mismos 4; el segundo 1/3, es decir 12; el tercero la mitad, 18. |
4+12+18=34. EL JUEZ SE LLEVA 2 |
|
PESAR NARANJAS |
Descubrimos la diferente en sólo dos pesadas: |
En la primera pesada ponemos 3 naranjas en cada platillo; con esto descubrimos si la diferente está en un platillo (la balanza se inclinará hacia ese lado o permanece en fiel y la diferente se encontrará en las 3 que quedaron sin pesar. |
En la segunda pesada ponemos 1 naranja en cada platillo; se inclinará la balanza hacia el lado de la diferente o permanecerá en fiel y será la que se quedó sin pesar. |
|
LAS BOTELLAS DE LECHE |
El primero: 3 llenas, 1 medio vacía y 3 vacías. (7 botellas, 3,5 litros) |
Segundo: 2 llenas, 3 medio vacías y 2 vacías (7 botellas, 3,5 litros) |
Tercero: 2 llenas, 3 medio vacías y 2 vacías (7 botellas, 3,5 litros) |
|
PASAR EL RIO |
1.-  Negro conductor + Negro no conductor;  Vuelve Negro Conductor. |
2.- Negro conductor + Negro no conductor;Vuelve Negro Conductor. |
3.- Dos blancos; vuelven Blanco + Negro No conductor |
4.- Blanco + Negro Conductor; Vuelven Blanco + Negro No Conductor |
5.- Dos Blancos; vuelve Negro Conductor |
6.- Negro Conductor + Negro No Conductor; vuelve Negro Conductor |
7.- Negro Conductor + Negro No Conductor |
|
REPARTIR EL VINO |
 |
|
| 1.- Llenamos la vasija de 5 arrobas. Quedan 3 en la de 8 | |
| 2.- Con la de 5 llenamos la de 3. Quedan 2 en la de 5 | |
| 3.- Vaciamos la de 3 en la de 8. Quedan 6 en la de 8 | |
| 4.- Ponemos las 2 de la 5 en la de 3. | |
| 5.- Llenamos la de 5 con la de 8. Queda 1 en la de 8 | |
| 6.- Llenamos la de 3 con la de 5. Quedan4 en la de 5 | |
| 7.-Pasamos los 3 de la de 3 a la de 8. La de 5 y la de 8 continen 4 cada una. | |
|
ERROR GRAMATICAL |
Falta el signo ; |
"Un pastor tenía un becerro y la madre; del pastor era el padre del becerro" |
|
HACE YA MUCHOS AÑOS... |
Llamando x, y, z respectivamente a cada clase de animales tendríamos 2 ecuaciones con 3 incógnitas, con lo cual tendríamos que asignar a una de ellas un valor fijo y resolver un montón de sistemas. |
Pero traduciendo el sistema a duros vemos que llamando x, por ejemplo, a los animales de 0,25 pts sólo puede ser múltiplo de 20, con lo cual sólo tendriamos que resolver los 4 sistemas siguientes: |
20*0,25 + 5*y + 25*z = 500 |
40*0,25 + 5*y + 25*z = 500 | 60*0,25 + 5*y + 25*z = 500 | 80*0,25 + 5*y + 25*z = 500 |
20 + y + z = 100 |
40 + y + z = 100 |
60 + y + z = 100 |
80 + y + z = 100 |
Los tres primeros no dan cocientes enteros, sino el último. Así obtendríamos x=80; y=1; z=19 |
80*0,25 + 1*5 + 19 * 25 = 20 + 5 + 475 =500; 80 + 1 + 19 = 100 |
|
PASAR LOS SAPOS. |
Asignando un número a cada sapo comenzando por la izquierda la secuencia de movimientos es la siguiente: |
3 - 4 - 5 - 3 - 2 - 1 - 4 - 5 - 6 - 3 - 2 - 1 - 5 - 6 - 1 |
|
Lo puso en marcha. Cuando llegó a casa del amigo observó la hora que marcaba el reloj. Al irse volvió a mirar el reloj para calcular el tiempo que había estado allí. Al volver a su casa vió el tiempo que habia estado fuera, restó el tiempo que había estado en casa de su amigo y dividió el resto entre dos (tiempo de ir y volver). Sabiendo la hora a la que salió de casa del amigo supo la hora exacta que tenía que marcar su reloj. |
|
EL PRESO |
La solución se basa en la regla de los signos: la verdad de una mentira o la mentira de una verdad siempre produce una mentira. Por tanto la pregunta que hay que hacer a cualquiera de ellos es "Si tu fueras el otro, ¿que camino me dirias? y elegir el camino contrario. |
|
TRIÁNGULOS RECTÁNGULOS O TEOREMA DE PITÁGORAS |
Aquí tienes varias series de DOS triángulos que cumplen la condición: |
12, 35, 37 y 20, 21, 29 (Superficie 210); 36, 105, 111 y 60, 63, 87(Superficie 1890); 28, 195, 197 y 60, 91, 109 (Superficie 2730) |
Y una de TRES: 15, 112, 113; 24, 70, 74 y 40, 42, 58 (Superficie 840) |
Si quieres ver más pulsa AQUÍ |
|
LAS GORRAS |
 |
|
Como puede observarse en el gráfico, de todas las combinaciones posibles sólo la 5, 6 y 7 contemplan que la gorra del tercero sea negra. |
|
| El caso 5 no puede darse porque habría acertado el primero. | |
| En el caso 6 habría acertado el segundo. (Ve 2 negras) | |
En el caso 7 también habría acertado el segundo puesto que el primero habría visto la negra del 3 y la del segundo. La del segundo tendría que ser blanca. |
|
| Así pues en los demás casos la del tercero es blanca | |
|
LAS TRES HIJAS |
Las edades son 9, 2 y 2 años Explicacioón: Los productos posibles de 36 y las sumas son: |
| 2 x 18 x 1 (21) | 2 x 2x 9 (13) | 4 x 9 x 1 (14) |
| 3 x 12 x 1 (16) | 6 x 6 x 1 (13) | 6 x 3 x 2 (11) |
El número de la casa de enfrente que están viendo es 11, 13 14, 16 o 21. Si fuera el 11, 14, 16 o 21 no necesitaria más datos. Si falta un dato es porque están viendo el 13. La mayor toca el piano es para indicar que los numeros son 2, 2, y 9 puesto en 6, 6 y 1 no hay una mayor sino dos (Tambíen podría haber dicho cualquier otra frase referente a la menor, en cuyo caso las edades serían 6, 6, 1 |
|
LA CUERDA |
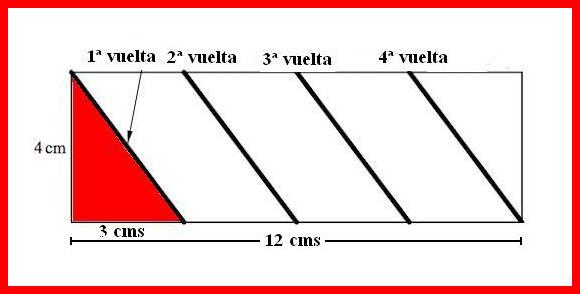
El problema sólo requiere el conocimiento del Teorema de Pitágoras e imaginación. |
Imaginemos que cortamos longitudinalmente la barra y la convertimos en una figura plana. Como podemos observar en el dibujo, cada vuelta de la cuerda mide 3 cms. En el triángulo coloreado la primera vuelta (y lógicamente todas las demás es la hipotenusa de un triángulo rectángulo de catetos 4 y 3 cms, Por tanto mide la raíz cuadrada de la suma de los cuadrados de los catetos es decir de 16 + 9. Así pues, la raiz de 25 es 5. Como da 4 vueltas la cuerda tendrá 20 cms de longitud. |
 |
|
LA CONTRASEÑA |
||||
| La contraseña consiste en decir el número de letras corespondiente al número que les dicen desde dentro | ||||
| Dieciocho tiene nueve letras. | ||||
| Ocho tiene cuatro letras. | ||||
| Catorce tiene siete. | ||||
| Cero tiene cuatro. | ||||
| Y seis tiene otras cuatro. | ||||
|
EL RELOJ |
||||
 |
||||
|
||||
LOS DOS BARBEROS |
||||
Al existir sólo dos barberos en la ciudad cada uno de ellos tenía que cortar el pelo al otro, por lo tanto el barbero pulcro era el que cortaba el pelo al desgreñado. El barbero desgrañado cortaba mejor el pelo que el pulcro. |
||||
|
||||
|
|
|
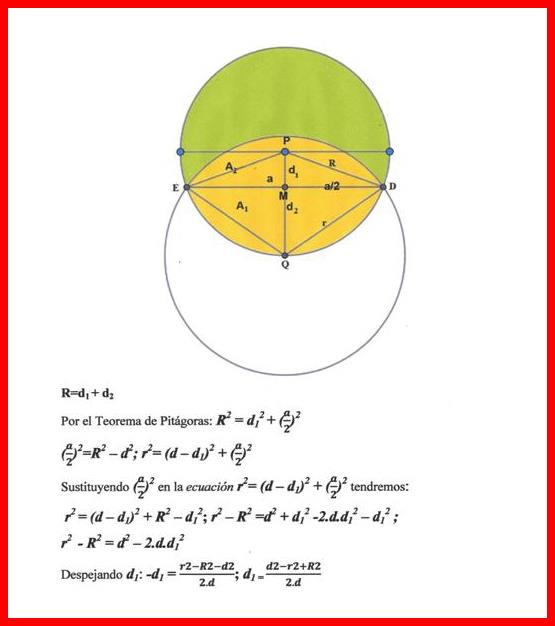
LA CABRA |
 |
 |
|
TELEGRAMA |
|
+ |
|
+ |
|
UNIR PUNTOS |
 |
 |
|
TRIÁNGULO |
 |
|
|
|||
|
